levenshtein-distance

利文斯坦 距离 简要来说：

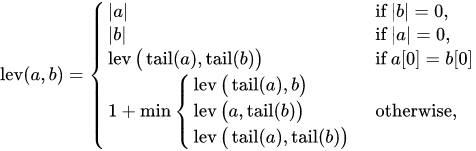
  1. b是空串，距离就是a的长度，反之亦然
  2. a[0] == b[0] ，则lev(a,b ) = lev(a[1:], b[1:])，即首字符相同，则忽略不计
  3. 如果a[0] != b[0]，则计1，再＋下面三个值的最小值：
    1. lev(a[1:], b)
    2. lev(a, b[1:])
    3. lev(a[1:], b[1:])

听起来很简单，可以写代码了，


int lev(std::string_view a, std::string_view b) {
    
    if(a.empty() || b.empty()) {
        return a.size() + b.size();
    }
    
    if(a[0] == b[0]) {
        return  lev(a.substr(1), a.substr(1));
    } else {
        int sub1 = lev(a.substr(1), b);
        int sub2 = lev(a.substr(1), b.substr(1));
        int sub3 = lev(a, b.substr(1));
        return 1 + std::min({sub1, sub2, sub3});
    }
}

如何用于搜索


const float limit = 0.5;

std::string s = "history";
std::string term = "hitory";

bool match(std::string &s, std::string & term) {
    return (float)lev(s, term)/ term.size()  < limit;
}

优化

实际试用了下，发现效率超级低，用于搜索app名字都被导致卡顿和风扇狂转。

最简单的优化就是超过一定距离后放弃。比如说超过搜索term长度一半的时候。